@TODO:
- 算法设计: 排序, 贪心, 分治, 动态规划, 回溯, 随机化
- 数学基础: 二分查找, 欧几里得算法, 快速幂算法
- 字符串匹配算法: KMP
- 图论算法:
- 拓扑顺序
- 最短路径: Dijkstra算法, Floyd-Warshall算法
- 最小生成树: Prim, Kruskal
- 搜索算法: BFS, DFS, A*搜索
- 几何算法: 向量, 凸包
- 快速傅里叶变换(FFT): 离散傅里叶变换
复杂度分析
数学基础回顾
- 几何级数: $$ 1 + 2^1 + 2^2 + … + 2^N = 2^(N+1) -1 ≈ 2^N $$
- 算术级数: $$ 1 + 2 + 3 + … + N = N(N+1)/2 ≈ N^2/2 $$
复杂度表示法
本节参考: 007函数的渐近的界 - 算法基础 | Coursera @Ref
▶ 大O符号(英语:Big O notation) 用另一个(通常更简单的)函数来描述一个函数数量级的渐近上界。 设函数 $f(n)$ 代表某一算法在输入大小为n的情况下的工作量(效率),我们将 $f(n)$ 与另一行为已知的函数 $g(n)$ 进行比较,如果存在正数 C 和 n0,使得对于一切 $ n >= n0 $ 有: $ 0 <= f(n) <= C g(n) $, 则可以称 $f(n)$ 的渐进上界是 $g(n)$,记做 $ f(n) = O(g(n)) $
可以理解为, 当n趋近于无穷大的时候, $ f(n) $ 和 $ C g(n) $ 是同一数量级的
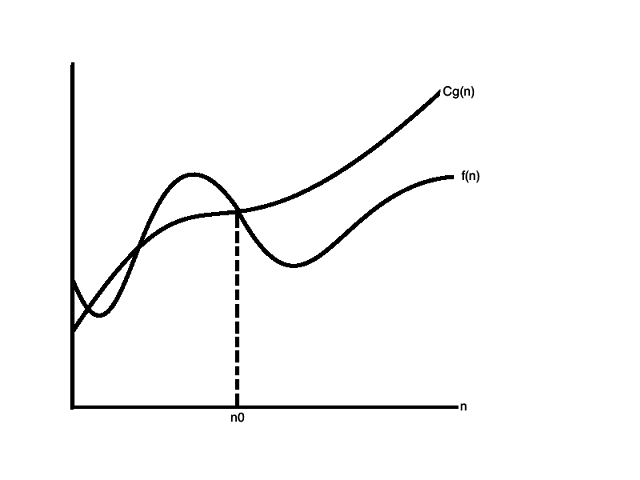
▶ 大Ω符号,读音:big omega,用另一个(通常更简单的)函数来描述一个函数数量级的「渐进下界」。如果存在正数 C 和 n0,使得对于一切 $ n >= n0 $ 有: $ 0 <= C g(n) <= f(n) $, 则可以称 $f(n)$ 的渐进下界是 $g(n)$,记做 $ f(n) = Ω(g(n)) $
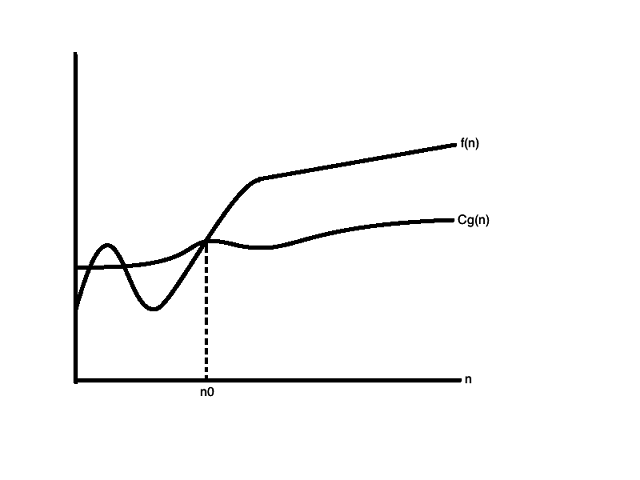
▶ 小O符号: 类似大O,也用来表示「渐近上界」,如过对于任意正数 C 和 n0,使得对于一切 $ n >= n0 $ 有: $ 0 <= f(n) < C g(n) $, 则可以称 $f(n)$ 的渐进下界是 $g(n)$,记做 $ f(n) = o(g(n)) $。 注意与大O定义的不同,「任意正数C」以及 $ f(n) < C g(n) $。
例如, $ f(n) = n^2 + n $,则 $ f(n) $ 的复杂度可以记为 $ o(n^3) $
常用算法复杂度分析
算法中 $log$ 级别的时间复杂度都是由于使用了分治思想, 这个底数直接由分治的复杂度决定:
- 如果采用二分法, 那么就是 $log_2 n$, 三分法就是 $log_3 n$, 其他亦然;
- 不过无论底数是什么, 对数函数的渐进趋势是一样的, 所以通常忽略底数只用 $logn$ 表示;
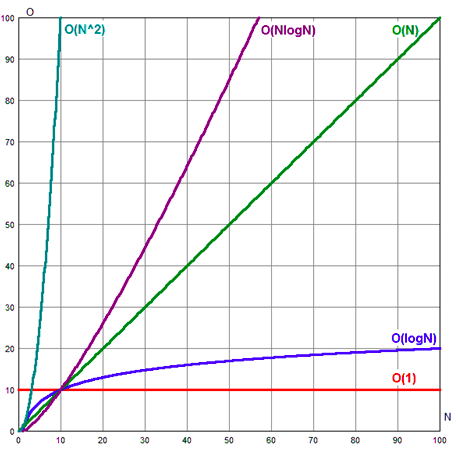
场景复杂度的增长趋势如下图: $O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)$
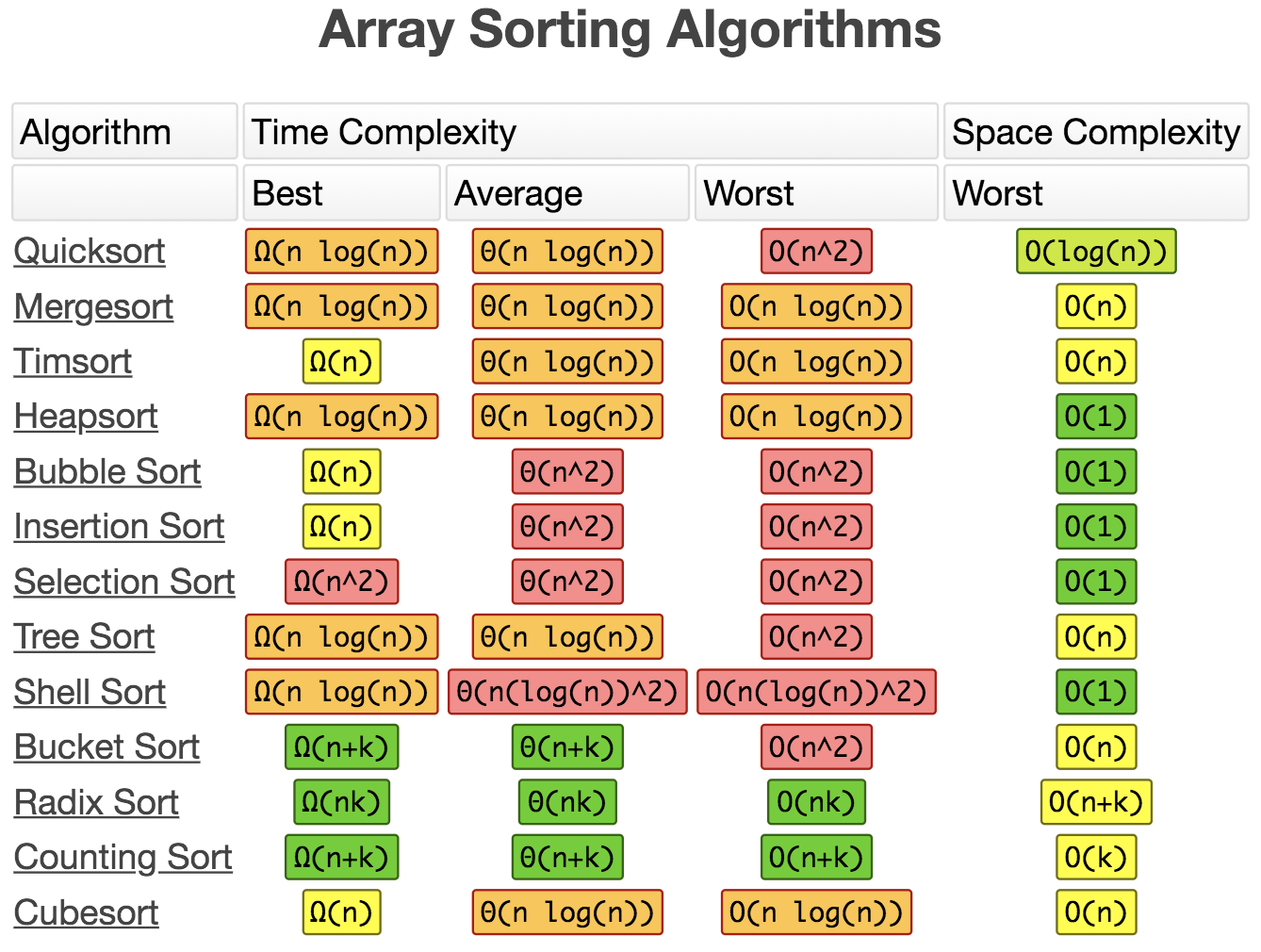
排序算法复杂度
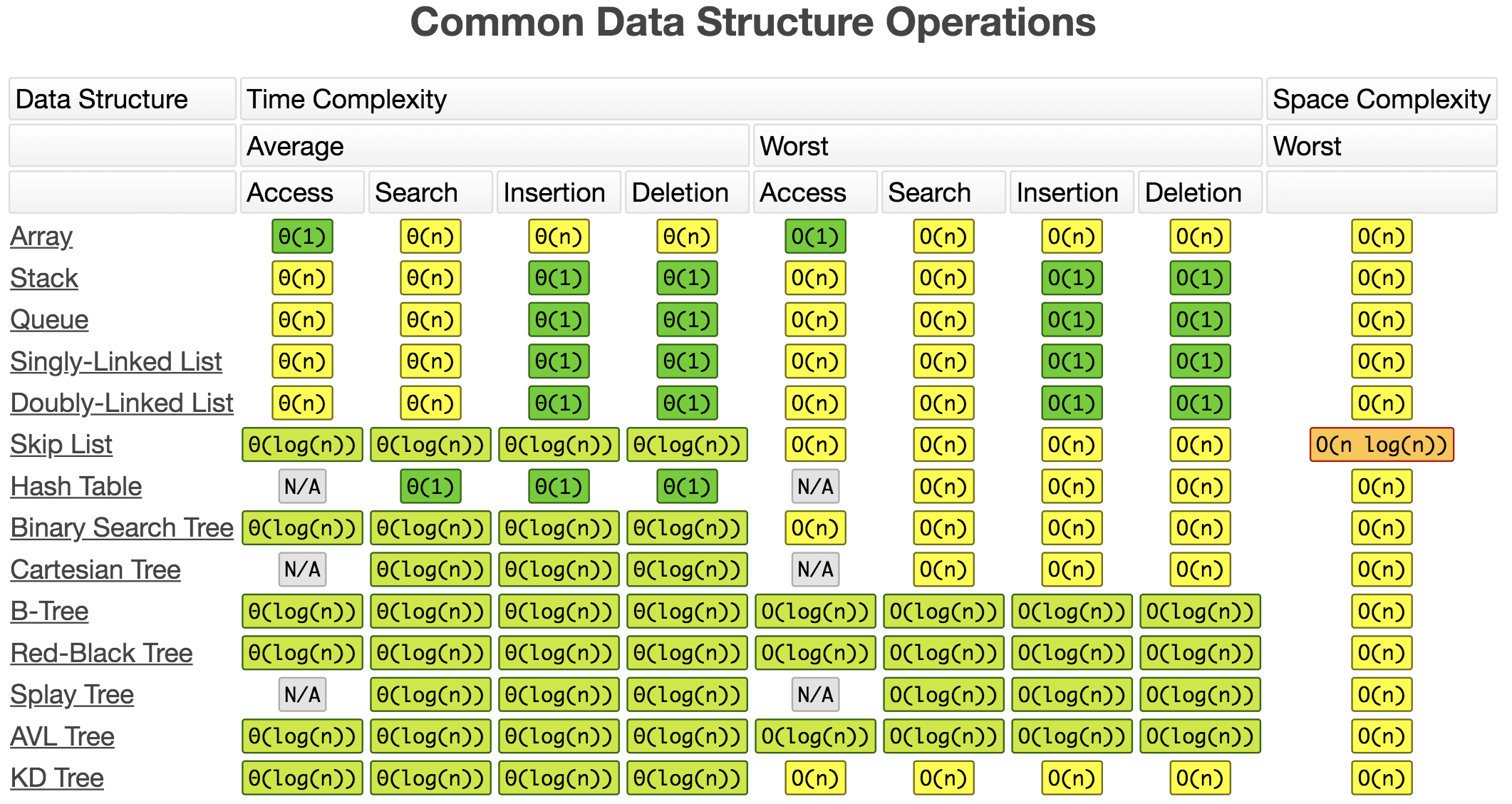
数据结构复杂度
Big-O Cheat
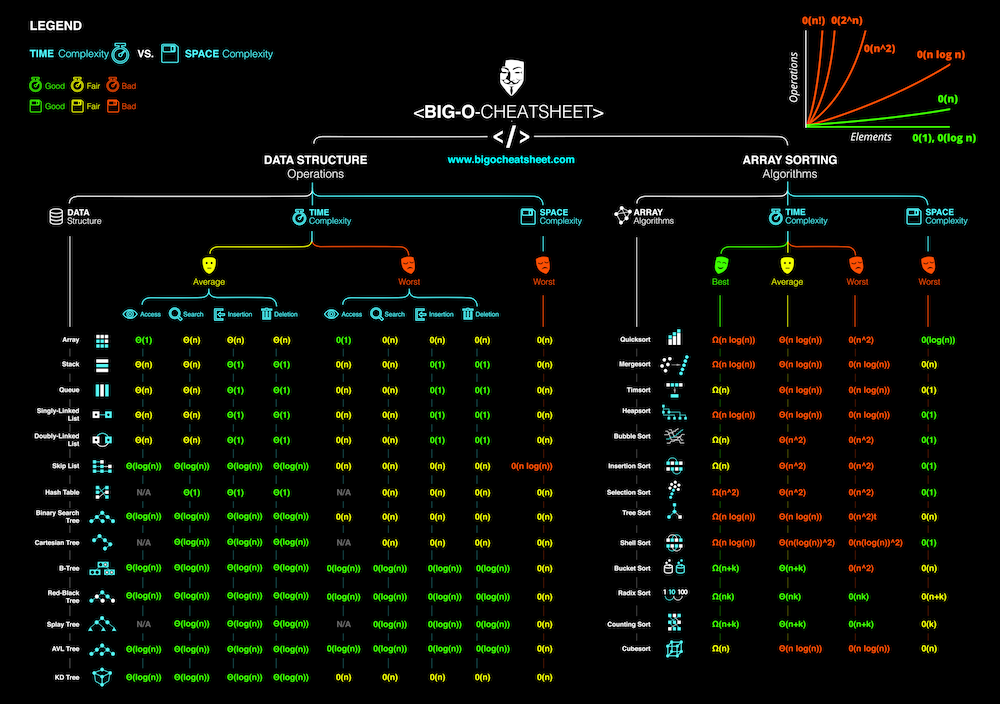
@Ref: Big-O Algorithm Complexity Cheat Sheet (Know Thy Complexities!) @ericdrowell
算法设计
贪婪
分治
二分查找:
int BinarySearch(int array[], int n, int value) |
回溯
@TODO
动态规划
图(Graph)
深度优先 & 广度优先
▶ 图(Graph)是一种灵活的数据结构,一般作为一种模型用来定义对象之间的关系或联系。对象由顶点(V)表示,而对象之间的关系或者关联则通过图的边(E)来表示。图可以分为有向图和无向图,一般用 $ G=(V,E) $ 来表示图。
▶ 深度优先(DFS) vs 广度优先(BFS)
- 深度优先 算法是一种优先遍历子节点而不是回溯的算法,时间复杂度: O(|V| + |E|)
- 广度优先 搜索是优先遍历邻居节点而不是子节点的图遍历算法,时间复杂度: O(|V| + |E|)
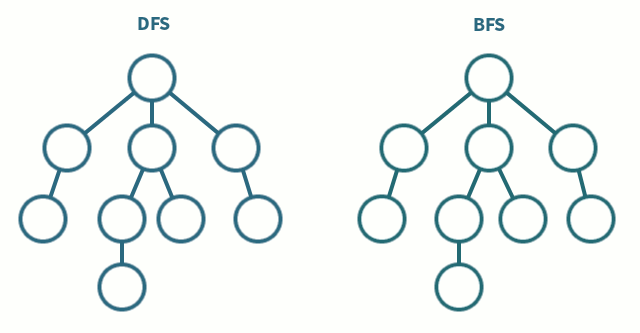
拓扑排序
@TODO
最短路径算法
@TODO
无权最短路径
@TODO
Dijkstra算法
@TODO
网络流问题
@TODO
最小生成树
@TODO